Διάλεξη:

1

2

3

4

5

6

7

4.3 Μέθοδοι επίλυσης γραμμικών διαφορικών εξισώσεων με γραμμικούς συντελεστές

Ορίζουμε τον διαφορικό τελεστή : D=d/dx και έχουμε:
L = anDn+ an-1Dn-1+...+ a0 = F(D)

Η διαφορική εξίσωση γράφεται F(D)y=R(x)

Για το ομογενές κομμάτι F(D)y=0, δοκιμάζουμε τη λύση 
κι έτσι καταλήγουμε στη χαρακτηριστική εξίσωση F(ρ)=0 με ρίζες ρ₁,ρ₂,...,ρ_n 

(I). Αν η F(ρ)=0 έχει n διαφορετικές ρίζες

Τότε η γενική λύση της ομογενούς είναι :

(II). Αν υπάρχει πολλαπλή ρίζα ρ₀ πολλαπλότητας r

Τότε στη ρίζα αυτή αντιστοιχούν οι λύσεις:

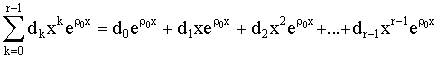
Για το μη ομογενές...

Εχουμε ειδική λύση:

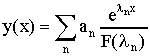
με την προυπόθεση το λ_n να είναι διάφορο των ριζών της χαρακτηριστικής εξίσωσης.

 

(III). Συντονισμός

Εστω ότι κάποιο απο τα λ_n ταυτίζεται με μια ρίζα του χαρακτηριστικού πολυωνύμου πολλαπλότητας r.
Στην ειδική λύση έχουμε (θέτοντας λ=λ_n):

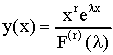
(IV). R(x)=πολυώνυμο

Πρέπει να γράψουμε το 1/F(D) σε μορφή σειράς:

 

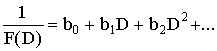
(V). R(x)=εκθετικό επί πολυώνυμο

 

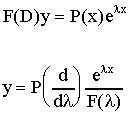
4.4 Μέθοδος μετασχηματισμού Laplace

Ορίζουμε: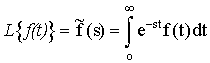   
Είναι γραμμικός μετασχηματισμός που μπορεί να μετατρέψει μία διαφορική εξίσωση σε μία αλγεβρική εξίσωση ως προς την άγνωστη συνάρτηση .Αφού μετασχηματίσουμε μία διαφορική εξίσωση κατά Laplace,λύνουμε ως προς την άγνωστη συνάρτηση και μετά, μέσω πινάκων,κάνουμε τον αντίστροφο μετασχηματισμό Laplace και βρίσκουμε την f(t).