Διάλεξη:

1

2

3

4

5

6

7

1. ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ

1.

Μία διαφορική εξίσωση (Δ.Ε.) είναι μία εξίσωση που περιέχει παραγώγους και της οποίας ο άγνωστος (άγνωστοι) είναι συναρτήσεις.

2.

Μία συνήθης Δ.Ε. (Σ.Δ.Ε.) περιέχει μόνο συνήθεις παραγώγους.

3.

Μία μερική Δ.E (M.Δ.E) περιέχει μερικές παραγώγους.

4.

Τάξη της Δ.Ε. είναι η τάξη της της ανώτερης παραγώγου της εξίσωσης.

5.

Στις γραμμικές Δ.Ε. η άγνωστη συνάρτηση και οι παράγωγοί της εμφανίζονται γραμμικά.

6.

Στις μη γραμμικές Δ.Ε. η άγνωστη συνάρτηση ή και οι άγνωστοί της,εμφανίζονται μη γραμμικά.

7.

Στις ομογενείς Δ.Ε. δεν υπάρχει όρος που να περιέχεί την άγνωστη συνάρτηση ή τις παραγώγους της.

8.

Στις μη ομογενείς Δ.Ε. εμφανίζεται όρος που εξαρτάται μόνο απο την ανεξάρτητη μεταβλητή.

9.

Στις γραμμικές και ομογενείς Δ.Ε. ισχύει η αρχή της επαλληλίας ή υπέρθεσης,δηλαδή ο γραμμικός συνδυασμός λύσεων είναι επίσης λύση της Δ.Ε.

10.

Λύση Δ.Ε. ονομάζεται μια οποιαδήποτε συνάρτηση η οποία επαληθεύει την Δ.Ε.

11.

Η γενική λύση περιέχει τόσες αυθαίρετες σταθερές,όση είναι και η τάξη της Δ.Ε.

12.

Μερική λύση είναι μια οποιαδήποτε λύση

13.

Ιδιάζουσα λύση δεν περιλαμβάνεται στη γενική λύση της Δ.Ε.

14.

Στις γραμμικές Δ.Ε. η γενική λύση δίνεται απο τη λύση της αντίστοιχης ομογενους συν μία οποιαδήποτε μερική λύση της πλήρους εξίσωσης.

 

2. ΕΞΙΣΩΣΕΙΣ ΠΡΩΤΗΣ ΤΑΞΗΣ

2.1 Γραμμική Δ.Ε.

Η γενική μορφή είναι : $$\frac{dx}{dy}+P(x)y=Q(x)$$
Λύνεται με τον ολοκληρωτικό παράγοντα μ=μ(x)
$$\mu y'+\mu Py=\mu Q \ \ (1)$$
Το αριστερό μέλος της (1) γίνεται τέλειο διαφορικό αν: 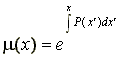$e^{\int^{x} P(x')dx'}$

Λύση:
$$y(x)=e^{\scriptscriptstyle -\int^{x}\!\! P(x')dx'} \int^{x}\!\! e^{\scriptscriptstyle \int^{x'}\!\! P(x'')dx''} Q(x')dx'$$

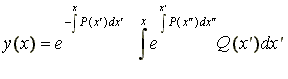
2.2 Διαχωρίσιμες Δ.Ε.

$$\frac{dx}{dy}=A(x)B(y)$$

Λύση:
$$\int^{y}\!\!\frac{dy'}{B(y')}=\int^{x}\!\!\frac{A(x')}{dx'}$$

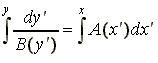
2.3 Ομογενείς Δ.Ε.

Μία συνάρτηση ονομάζεται ομογενής όταν ισχύει:
$$F(\lambda x,\lambda y)={\lambda}^d F(x,y)$$, όπου λ αυθαίρετη ποσότητα

Ο εκθέτης d λέγεται βαθμός ομοιογένειας της F.
$$\frac{dx}{dy}=f(\frac{y}{x})$$
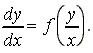
Η συνάρτηση f είναι ομογενής.Η αντικατάσταση μετατρέπει την
παράγωγο και η Δ.Ε. γίνεται διαχωρίσιμη:
$$u'=\frac{1}{x}(f(u)-u)$$