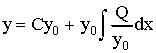Διάλεξη:

1

2

3

4

5

6

7

2.6 Ακριβείς Διαφορικές Εξισώσεις (Exact Differential Equations)

Η Διαφορική Εξίσωση:  
μπορεί να γραφεί σαν ολικό διαφορικό αν ισχύει:  

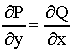
Αν όμως δεν ισχύει αυτή η σχέση,τότε μπορεί να αναζητηθεί ολοκληρωτικός παράγοντας μ=μ(x,y),τέτοιος ώστε μPdx+μQdy=0.
Ο ολοκληρωτικός παράγοντας μ βρίσκεται απο τη σχέση: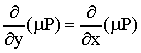  
η οποία στη γενική περίπτωση μ=μ(x,y),είναι μια εξίσωση με μερικές παραγώγους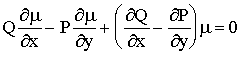 

Η εξίσωση αυτή απλοποιείται αν θεωρήσουμε το μ σαν συνάρτηση του x ή του y μόνο.

Γεωμετρική ερμηνεία

Η Διαφορική Εξίσωση  Pdx+Qdy=0  είναι ισοδύναμη με το πρόβλημα εύρεσης των ορθογωνίων τροχιών g(x,y) της δοσμένης οικογένειας καμπυλών f(x,y).

Υπενθυμίζουμε ότι:

α)

β)

γ)

Η συνθήκη εύρεσης της g(x,y) δίνεται απο τη συνθήκη καθετότητας ανάμεσα στο διάνυσμα (f_y',f_x) και το διάνυσμα dr της g(x,y),δηλαδή το εσωτερικό τους γινόμενο να είναι μηδέν:

(dx,dy)(f_y'-f_x)=0

Η λύση αυτής της Δ.Ε. μας δίνει τα σημεία (x,y) που συνιστούν την οικογένεια καμπυλών g(x,y) η οποία είναι κάθετη στη δοσμένη οικογένεια καμπυλών f(x,y).

2.7 Επίλυση Δ.Ε. πρώτης τάξης με τη μέθοδο μεταβολής σταθερών

(α)  Εστω y₀(x) η λύση της ομογενούς Δ.Ε.Δηλαδή της 

(β)  Θεωρούμε τη λύση: y=A(x)y₀(x), όπου A(x) άγνωστη συνάρτηση.
       Αντικαθιστούμε στην πλήρη εξίσωση,οπότε:

       

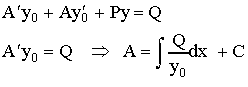
      Γενική λύση: